【2024(令和6)年度 新潟県公立高校入試】数学〔1〕小問集合 徹底解説！

\begin{eqnarray}3-12+7&=&3+7-12\\&=&10-12\\&=&-2\end{eqnarray}

\begin{eqnarray}3-12+7&=&-9+7\\&=&-2\end{eqnarray}

\begin{eqnarray}3(2a-b)-5(-a+2b)&=&6a-3b+5a-10b\\&=&6a+5a-3b-10b\\&=&11a-13b\end{eqnarray}

\begin{eqnarray}18xy^2\div(-3y)^2&=&18xy^2\div9y^2\\&=&\displaystyle\frac{18xy^2}{9y^2}\\&=&2x\end{eqnarray}

$$\displaystyle\frac{3}{10} , \frac{\sqrt{2}}{5} , \frac{1}{\sqrt{10}}$$

分母を\(10\)に揃えたいので、\(\displaystyle\frac{\sqrt{2}}{5}\)の分母分子を2倍します。

$$\displaystyle\frac{\sqrt{2}}{5} = \frac{2\sqrt{2}}{10}$$

\(\displaystyle\frac{1}{\sqrt{10}}\)は分母を有理化します。

$$\displaystyle\frac{1}{\sqrt{10}} = \frac{\sqrt{10}}{10} $$

これで分母が10に揃ったので後は分子の大きさを比べるだけです。

$$\displaystyle\frac{3}{10} , \frac{2\sqrt{2}}{10} , \frac{\sqrt{10}}{10}$$

\(2\sqrt{2} = \sqrt{8}\)、\(3 = \sqrt{9}\)なので、これらを分子が小さいもの順に並べると

$$\displaystyle\frac{\sqrt{8}}{10}\lt\frac{\sqrt{9}}{10}\lt\frac{\sqrt{10}}{10}$$

最後にそれぞれの数字を元の書き方に戻して答えとなります。

$$\displaystyle\frac{\sqrt{2}}{5}\lt\frac{3}{10}\lt\frac{1}{\sqrt{10}}$$

$$\displaystyle\frac{3}{10} , \frac{\sqrt{2}}{5} , \frac{1}{\sqrt{10}}$$

初手ですべてを2乗することで根号をなくします。

$$\displaystyle\frac{9}{100} , \frac{2}{25} , \frac{1}{10}$$

通分して分母を100に揃えます。

$$\displaystyle\frac{9}{100} , \frac{8}{100} , \frac{10}{100}$$

これらを分子が小さいもの順に並べると

$$\displaystyle\frac{8}{100}\lt\frac{9}{100}\lt\frac{10}{100}$$

元の形に戻して終わりです。

$$\displaystyle\frac{\sqrt{2}}{5}\lt\frac{3}{10}\lt\frac{1}{\sqrt{10}}$$

\begin{eqnarray}(x+5)^2 &=& 13\\ x+5 &=& \pm\sqrt{13}\\ x &=& -5\pm\sqrt{13}\end{eqnarray}

\begin{eqnarray}(x+5)^2 &=& 13\\ x^2+10x+25 &=& 13\\ x^2+10x+12 &=& 0\\ x &=& \displaystyle\frac{-10\pm\sqrt{10^2-4\times1\times12}}{2\times1}\\ &=& \frac{-10\pm\sqrt{100-48}}{2}\\ &=& \frac{-10\pm\sqrt{52}}{2}\\ &=& \frac{-10\pm2\sqrt{13}}{2}\\ &=& -5\pm\sqrt{13}\end{eqnarray}

食品が温まるまでの時間を\(y\)分、電子レンジの出力を\(x\)Wとすると、

$$\displaystyle y = \frac{a}{x}$$

と表わされる。これを\(a\)について整理すると

$$a = xy $$

500Wでの加熱時間が3分なので、この式に\(x=500\) , \(y=3\)を代入すると

$$a = 500\times3 = 1500$$

したがって、この反比例の式は \(\displaystyle y = \frac{1500}{x}\)だとわかる。

600Wでの加熱時間(\(y\))はこの式に\(x=600\)を代入することで求められるので

$$\displaystyle y = \frac{1500}{600} = \frac{5}{2} $$

\(\displaystyle\frac{5}{2}\)分は\(2.5\)分(\(1\)\(\displaystyle\frac{1}{2}\)分)、\(0.5\)分(\(\displaystyle\frac{1}{2}\)分)は\(30\)秒。

よって求める時間は、2分30秒。

半円の中心をOとし、半径OCを結びます。

そうやってできた中心角\(\angle\)BOCの大きさを\(a\)とし、等しい線分や角に印をつけると以下のようになります。

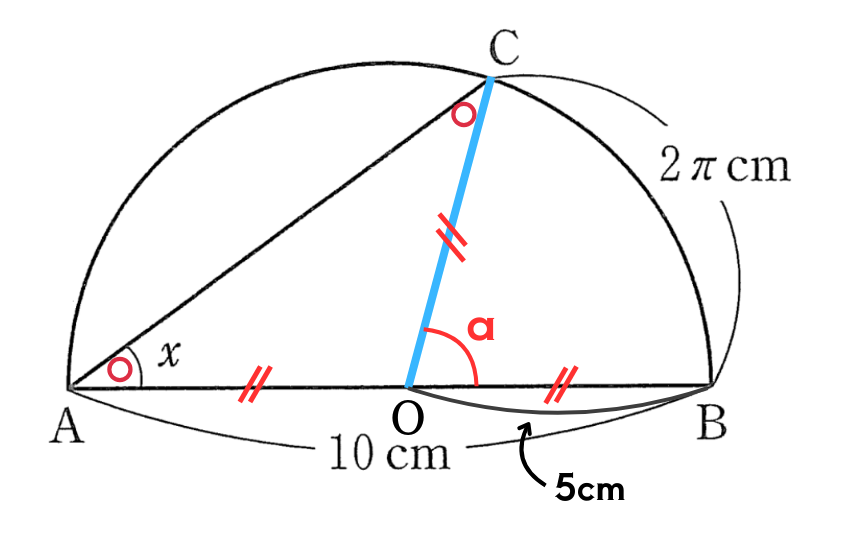
このように書き込むことができたらあとは順番に角の大きさを求めていきましょう！

\(\angle a\)の大きさを求めます。

ここは半径5cm、この長さ2\(\pi\)cmのおうぎ形の中心角です。

おうぎ形の中心角の求め方はいくつかありますが、今回は弧の長さについての方程式を作って求めてみましょう。

中心角\(a^{\circ}\)のおうぎ形の弧の長さは、直径 \(\times \pi \times \displaystyle\frac{a}{360}\)で求められます。

この公式を左辺で使い、弧の長さは\(2\pi\)なのでこれを右辺に置くと

$$10 \times \pi \times \displaystyle\frac{a}{360} = 2\pi$$

このような方程式を作ることができますので、これを解きます。

10と360を約分して、両辺を\(\pi\)で割って\(\pi\)を消去すると

$$\displaystyle\frac{a}{36} = 2$$

両辺に36を掛けます。

$$a = 2 \times 36 = 72$$

よって、\(a=72^{\circ}\)です。

求める\(\angle x\)は\(\stackrel{\huge\frown}{BC}\)に対する円周角で、いま求めた\(\angle a\)は同じ弧に対する中心角になります。

同じ弧に対する円周角は中心角の\(\displaystyle\frac{1}{2}\)なので、

$$\angle x = 72 \times \displaystyle\frac{1}{2} = 36$$

したがって、\(\angle x = 36^{\circ}\)。

箱の中に入っている白玉の個数を\(x\)個とすると、箱の中には白玉\(x\)個と赤玉300個が入っています。

標本として取り出した100個の玉のうち、10個が赤玉だったので残りの90個は白玉です。

つまり、標本における白玉と赤玉の個数の比は\(90 : 10 = 9 : 1\)になります。

この比と箱の中にある白玉と赤玉の個数の比が等しくなるので、次のような比例式が成り立ちます。

$$ x : 300 = 9 : 1$$

これを解くと、\(x = 2700\)

したがって箱の中に入っている白玉の数は、およそ2700個。

箱の中に入っている白玉の個数を\(x\)個とすると、箱に入っている玉の個数は\(x+300\)個と表されます。

よって母集団全体とそこに含まれる赤玉の個数の比は、\(x+300 : 300\)

また、標本として取り出した100個の玉のうち10個が赤玉だったので、標本全体とそこに含まれる赤玉の個数の比は、\(100 : 10 = 10 : 1\)

この2つの比が等しくなるので、次のような比例式が成り立ちます。

$$ x+300 : 300 = 10 : 1$$

これを解くと

\begin{eqnarray}x+300 &=& 3000\\ x &=& 3000–300\\ &=& 2700\end{eqnarray}

したがって箱の中に入っている白玉の数は、およそ2700個。